想象你站在一条宽阔的河流边,看着水流缓缓流淌。你是否想过,如何精准测量这条河流的流量呢?在水利工程、环境监测、农业灌溉等领域,明渠流量的精确测量至关重要。而超声波明渠流量计,就是实现这一目标的得力工具。它利用超声波技术,非接触式地测量水位,再通过一系列计算公式,将水位信息转化为流量数据。今天,就让我们一起深入了解超声波明渠流量计的计算公式,探索其背后的科学原理。
超声波明渠流量计的工作原理

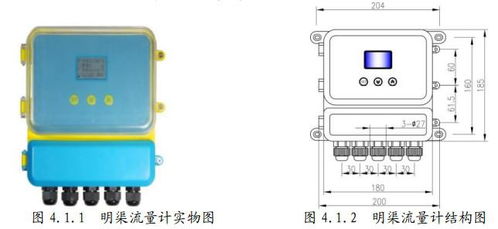
超声波明渠流量计的核心原理是超声波回声测距。它由仪表主机和超声波探头组成,探头安装在量水堰槽水位观测点上方。当探头向水面发射超声波时,声波会被水面反射回来,探头接收到回声后,记录下声波传输的时间。通过这个时间,结合超声波在空气中的传播速度,就可以计算出液位高度。
具体来说,超声波测液位的高度计算公式如下:
\\[ H = \\frac{L - D - \\frac{V_T}{2}}{L - \\frac{(V_0 + a \\cdot t)T}{2}} \\]
其中:
- \\( H \\) 表示液位高度
- \\( L \\) 表示超声探头与明渠底部之间的距离
- \\( D \\) 表示超声波探头到水面的垂直距离
- \\( V \\) 表示空气中的超声波声速
- \\( T \\) 为超声波一个回程经过的时间
- \\( V_0 \\) 表示 0℃时超声波在空气中的传播速度
- \\( a \\) 为超声波速度的温度系数
- \\( t \\) 为温度
这个公式看似复杂,但实际应用中,仪表主机会自动完成这些计算,用户只需读取结果即可。不过,了解这些参数的意义,有助于我们更好地理解超声波明渠流量计的工作原理。
量水堰槽与水位-流量关系

超声波明渠流量计直接测量的物理量是液位,但要得到流量数据,还需要知道水位与流量之间的关系。这就要依靠量水堰槽了。量水堰槽是一种特殊的结构,它能够将明渠内的流量大小转化为液位的高低。常见的量水堰槽有直角三角堰、矩形堰和巴歇尔槽等。
不同的量水堰槽有不同的水位-流量关系计算公式。例如,直角三角堰的水位-流量关系公式为:
\\[ Q = \\frac{2}{3} \\cdot \\sqrt{2g} \\cdot \\tan\\left(\\frac{\\theta}{2}\\right) \\cdot H^{5/2} \\]
其中:
- \\( Q \\) 表示流量
- \\( g \\) 表示重力加速度
- \\( \\theta \\) 表示堰口角度
- \\( H \\) 表示堰上水头
而矩形堰的水位-流量关系公式为:
\\[ Q = \\frac{2}{3} \\cdot \\sqrt{2g} \\cdot b \\cdot H^{5/2} \\]
其中:
- \\( b \\) 表示堰口宽度
巴歇尔槽的水位-流量关系则更为复杂,需要根据具体的槽体尺寸和形状进行计算。这些公式都可以在国家计量检定规程《明渠堰槽流量计》JJG711-90中找到。
超声波明渠流量计的计算公式
在了解了量水堰槽与水位-流量关系后,我们再来看超声波明渠流量计的计算公式。实际上,超声波明渠流量计的计算公式可以简化为以下几个步骤:
1. 测量液位高度:利用超声波回声测距原理,计算出液位高度 \\( H \\)。
2. 确定水位-流量关系:根据量水堰槽的种类和尺寸,找到对应的水位-流量关系公式。
3. 计算流量:将液位高度 \\( H \\) 代入水位-流量关系公式,计算出流量 \\( Q \\)。
例如,如果使用的是直角三角堰,那么流量 \\( Q \\) 的计算公式就是:
\\[ Q = \\frac{2}{3} \\cdot \\sqrt{2g} \\cdot \\tan\\left(\\frac{\\theta}{2}\\right) \\cdot H^{5/2} \\]
这个公式看似简单,但实际应用中,仪表主机会自动完成这些计算,用户只需读取结果即可。不过,了解这些参数的意义,有助于我们更好地理解超声波明渠流量计的工作原理。
超声波明渠流量计的应用领域
超声波明渠流量计因其非接触式测量、高精度、可靠性高等优点,广泛应用于多个领域。以下是一些主要的应用场景:
1. 水利工程:在水库、河流、灌溉渠等水利工程中,超声波明渠流量计可以实时监测流量,为水资源管理提供数据支持。


